class="markdown_views prism-atom-one-light">

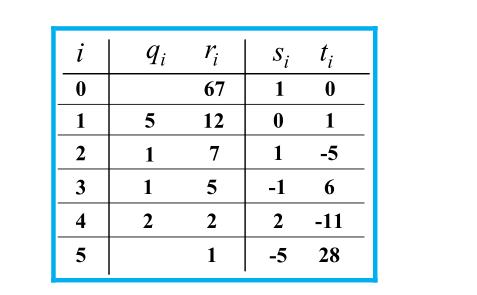
 首先对67和12进行辗转相除法计算(67除12的商为5 余数为7 12除7的商为1 余数为5 ……),一直辗转相除,直到余数为1,这时 t 列的最后一个就是我们所求的答案,为28.
这里我们一般来说直接求 t 列就可以了,s列可以不求。s 列的第0行和第1行的值固定为1和0,t 列的第0行和第1行的值固定为0和1,所以我们直接从2行开始计算。
首先对67和12进行辗转相除法计算(67除12的商为5 余数为7 12除7的商为1 余数为5 ……),一直辗转相除,直到余数为1,这时 t 列的最后一个就是我们所求的答案,为28.
这里我们一般来说直接求 t 列就可以了,s列可以不求。s 列的第0行和第1行的值固定为1和0,t 列的第0行和第1行的值固定为0和1,所以我们直接从2行开始计算。
通过列表法求模逆的理论基础
注意:求模逆的两个数必须互素


计算方法:
 首先对67和12进行辗转相除法计算(67除12的商为5 余数为7 12除7的商为1 余数为5 ……),一直辗转相除,直到余数为1,这时 t 列的最后一个就是我们所求的答案,为28.
这里我们一般来说直接求 t 列就可以了,s列可以不求。s 列的第0行和第1行的值固定为1和0,t 列的第0行和第1行的值固定为0和1,所以我们直接从2行开始计算。
首先对67和12进行辗转相除法计算(67除12的商为5 余数为7 12除7的商为1 余数为5 ……),一直辗转相除,直到余数为1,这时 t 列的最后一个就是我们所求的答案,为28.
这里我们一般来说直接求 t 列就可以了,s列可以不求。s 列的第0行和第1行的值固定为1和0,t 列的第0行和第1行的值固定为0和1,所以我们直接从2行开始计算。
t2=t0-q1*t1 即 -5=0-5*1;
t3=t1-q2*t2 即 6=1-1*(-5);
t4=t2-q3*t3 即 -11=(-5)-1*6;
t5=t3-q4*t4 即 28=6-2*(-11);
通过Java实现的代码
/**
* 求一个数的逆
*
* @author 汪书北
*
*/
public class Inversion {
public static void main(String[] args) {
// 求逆
long a = inversion(12, 221);
System.out.println(a);
}
/**
* a*b=1 mod n 结果返回b 即 a的逆元
*
* @param a
* @param n
* @return
*/
public static long inversion(long a, long n) {
//保存n的值
long n1=n;
// 检测两个数是否互素,不互素返回-1,互素返回辗转相除的次数
int length = gcdJC(a, n);
// 如果不互素 返回-1
if (length == -1)
return -1;
if (a > n)
length += 2;// 如果a比模数大,则数组长度加2
long[] t = new long[length];
// 初始化
t[0] = 0;
t[1] = 1;
int i = 0;
long temp1 = 0, temp2 = 0;
while (true) {
temp1 = n / a;
temp2 = n % a;
i++;
t[i + 1] = t[i - 1] - temp1 * t[i];
if (temp2 != 1) {
n = a;
a = temp2;
} else {
if (t[length - 1] < 0)
return t[length - 1]+n1;//如果为负数加上模数 变为正数
else
return t[length - 1];
}
}
}
/**
* 检测两个数是否互素,不互素返回-1,互素返回辗转相除的次数
*
* @param a
* @param b
* @return 不互素返回-1,互素返回辗转相除的次数
*/
public static int gcdJC(long a, long b) {
long r;
int i = 0;
while (b != 0) {
r = a % b;
i++;
if (r != 0) {
a = b;
b = r;
} else {
if (b == 1)
return i;
else
return -1;
}
}
return 0;
}
}