一、相关定理介绍1.乘法逆元
如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。下文中,x都表示乘法逆元。2.费马小定理假如a是一个整数,p是一个质数,那么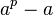 是p的倍数,可以表示为
是p的倍数,可以表示为
如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。下文中,x都表示乘法逆元。2.费马小定理假如a是一个整数,p是一个质数,那么
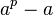 是p的倍数,可以表示为
是p的倍数,可以表示为
- 或者写作:
- 3.扩展欧几里得定理
- 已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式
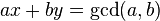 。
。 - 二、乘法逆元的求法
- 1.费马小定理
- 由费马小定理 ap-1≡1 , 变形得 a*ap-2≡1(mod p),答案已经很明显了:若a,p互质,因为a*ap-2≡1(mod p)且a*x≡1(mod p),则x=ap-2(mod p),用快速幂可快速求之.
- 2.扩展欧几里得
- 我们都知道模就是余数,比如12%5=12-5*2=2,18%4=18-4*4=2。(/是程序运算中的除)那么ax≡1 (mod p)即ax-yp=1.把y写成+的形式就是ax+py=1,为方便理解下面我们把p写成b就是ax+by=1。就表示x是a的模b乘法逆元,y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。
- 三、乘法逆元与除法取模
- 求a/b=x(mod M)只要M是一个素数,而且b不是M的倍数,就可以用一个逆元整数b1,通过 a/b=a*b1 (mod M),只能来以乘换除。
费马小定理:对于素数 M 任意不是 M 的倍数的 b,都有:b ^ (M-1) = 1 (mod M)
于是可以拆成:b*b^(M-2)=1(mod M)
于是:a/b=a/b*(b * b ^ (M-2))=a*(b ^ (M-2)) (mod M)求a/b=x(mod M)用扩展欧几里德算法算出b1,然后计算a*b1(mod M)exgcd(b,M,x,y); b1=x; 当p是个质数的时候有
inv(a) = (p - p / a) * inv(p % a) % p 证明:设x = p % a,y = p / a
于是有 x + y * a = p
(x + y * a) % p = 0
移项得 x % p = (-y) * a % p
x * inv(a) % p = (-y) % p
inv(a) = (p - y) * inv(x) % p
于是 inv(a) = (p - p / a) * inv(p % a) % p然后一直递归到1为止,因为1的逆元就是1