求同余方程x^A=B(mod m)的解个数(原根与指标)

分类： 数论2013-08-05 16:11 132人阅读 评论(0) 收藏 举报 求方程：的解个数
分析：设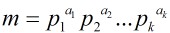，那么上述方程解的个数就与同余方程组：的解等价。
设同于方程的解分别是：，那么原方程的解的个数就是
所以现在的关键问题是求方程：的解个数。
这个方程我们需要分3类讨论：
第一种情况：
对于这种情况，如果方程的某个解设为，那么一定有，可以得到，即
所以方程的解个数就是：，也就是

第二种情况：
这样也就是说p|B，设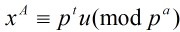，，本方程有解的充要条件是A|t， 那么我们设t=kA，
所以进一步有：，因为，这样又转化为第三种情况了。

第三种情况：
那么我们要求指标；求指标的话又要求原根。并且奇素数p的原根也是p^a的原根，所以说求个p的原根就好了。

且如果有解，则解的个数为(A,φ(p^a))。
求指标的话就是要解决A^x ≡ B (mod p^a)的问题。由于本情况保证了(p^a, B)=1，用个Baby-step-Giant-step就 能解决问题。
方程x^A ≡ B (mod p^a)有解，当且仅当(A,φ(p^a))|ind B。ind B表示B对于p^a的任一原根的指标。



如果不知道原根与指标的现在就补一下吧：
原根部分：
定义一：设m>1,(a,m)=1,则使得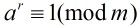成立的最小正整数r，称为a对模m的指数，或者a对模m的阶，记为
定理一：若m>1，(a,m)=1,,则
定义二：若，则a是模m的原根。
定理二：如果大于1的正整数m有原根，那么它一共有个不同的原根。
定理三：模m有原根的必要条件是m=2，4，p^a或者2p^a，其中p是奇素数。
定理四：设m>1,所有不同的奇因数是，(g,m)=1，则g是模m的原根的充要条件是：    1<=i<=k


指标，n次剩余部分：
现在我们来研究同余式  (a,m)=1，有解的条件以及解数，注意现在的m=p^a或者2p^a，，g是模m的一个原根。
若(n,c)=d ,(a,m)=1，则上述同余式有解的充要条件是d|inda，并且在有解的条件下，解数为d。
在模m的一个简化剩余系中，n次剩余的个数是


定理一：若r通过模c的最小非负完全剩余系，则g^r通过模m的一个简化剩余系。
证明：g是模m的一个原根，则对模m两两不同余，又因为(g,m)=1，所以(g^r,m)=1 因此是模m的一个简化剩余系。
定理一：设a是一整数，(a,m)=1，若对模m的一个原根g，有一整数r存在使得下式


成立，则r就叫做以g为底的a对模m的一个指标,记为r=inda。

经典题目：HDU3731

解高次同余方程(离散对数->扩展Baby Step Giant Step)

分类： 数论2013-02-12 20:04 125人阅读 评论(0) 收藏 举报 扩展Baby Step Giant Step深入学习请戳这里   题目：Clever Y   求解A^x = B (mod C) 中 0 <= x < C 的解。 本算法的安全性更高。 [cpp] view plaincopy

1. #include  
2. #include  
3. #include  
4. #include  
5.   
6. #define CC(m ,what) memset(m , what , sizeof(m))  
7.   
8. typedef long long LL ;  
9.   
10. LL A, B ,C ;  
11.   
12. const int NN=99991 ;  
13.   
14. bool hash[NN];  
15. int idx[NN];  
16. int val[NN];  
17.   
18. void insert(int id , LL vv)  
19. {  
20.     LL v = vv % NN ;  
21.     while( hash[v] && val[v]!=vv)  
22.     {  
23.         v++ ;  
24.         if(v == NN)  
25.            v-=NN ;  
26.     }  
27.     if(!hash[v])  
28.     {  
29.         hash[v] = 1;  
30.         val[v] = vv ;  
31.         idx[v] = id ;  
32.     }  
33. }  
34.   
35. int find(LL vv)  
36. {  
37.     LL v = vv % NN ;  
38.     while( hash[v] && val[v]!=vv)  
39.     {  
40.         v++ ;  
41.         if(v == NN) v-=NN;  
42.     }  
43.     if( !hash[v] ) return -1;  
44.     return idx[v];  
45. }  
46. void ex_gcd(LL a , LL b , LL& x , LL& y)  
47. {  
48.     if(b == 0)  
49.     {  
50.         x = 1 ;  
51.         y = 0 ;  
52.         return;  
53.     }  
54.     ex_gcd(b ,a%b,x,y);  
55.     LL t = x;  
56.     x = y;  
57.     y=t-a/b*y ;  
58. }  
59.   
60. LL gcd(LL a,LL b){  
61.     while( a%b != 0){  
62.         LL c = a ;  
63.         a = b ;  
64.         b = c % b ;  
65.     }  
66.     return b ;  
67. }  
68. LL baby_step(LL A, LL B , LL C)  
69. {  
70.     LL ans = 1 ;  
71.     for(LL i=0;i<=50;i++)  
72.     {  
73.         if(ans == B)    return i ;  
74.         ans = ans * A % C ;  
75.     }  
76.     LL tmp , d = 0 ;  
77.     LL D = 1 % C ;  
78.     while( (tmp=gcd(A,C)) != 1 )  
79.     {  
80.         if(B % tmp) return -1 ;  
81.         d++ ;  
82.         B/=tmp ;  
83.         C/=tmp ;  
84.         D = D*A/tmp%C ;  
85.     }  
86.     CC( hash , 0) ;  
87.     CC( idx, -1) ;  
88.     CC(val , -1) ;  
89.     LL M = ceil( sqrt(C*1.0) ) ;  
90.     LL rr = 1 ;  
91.     for(int i=0;i
92.     {  
93.         insert(i, rr) ;  
94.         rr = rr * A % C ;  
95.     }  
96.     LL x, y ;  
97.     for(int i=0;i
98.     {